Закон Ома для полной цепи и для участка цепи: варианты записи формулы, описание и объяснение

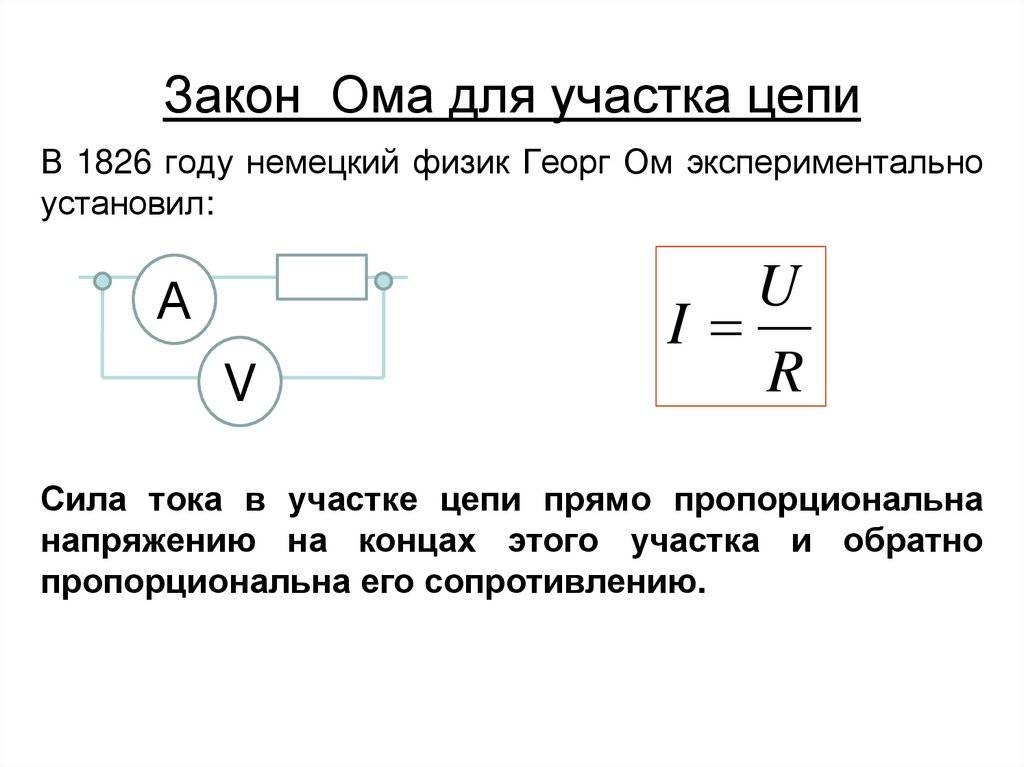
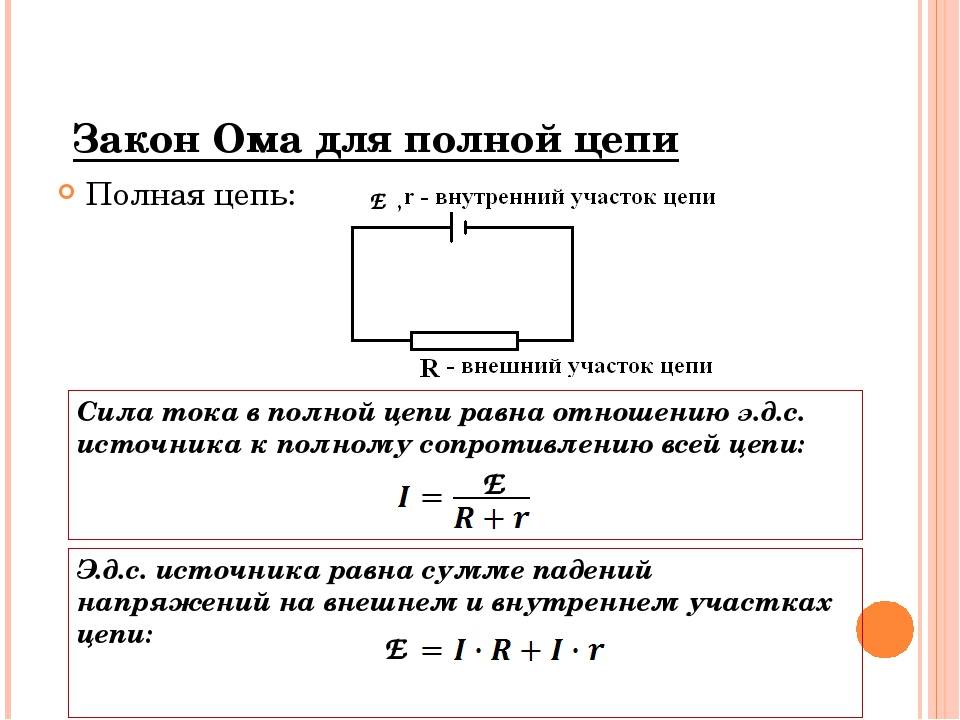
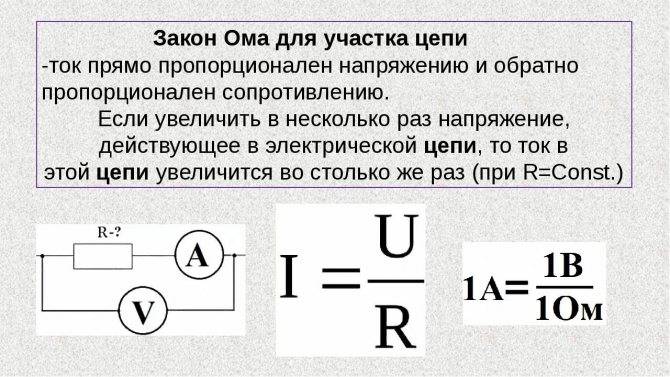
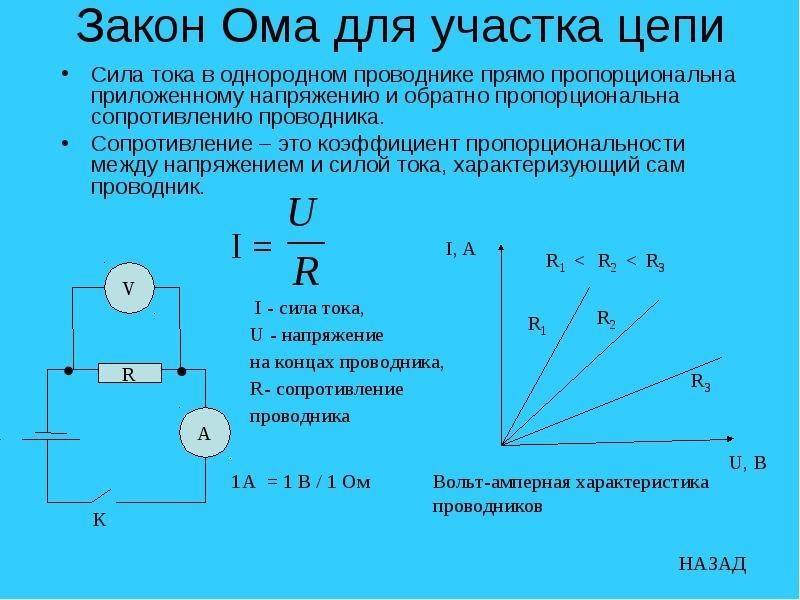
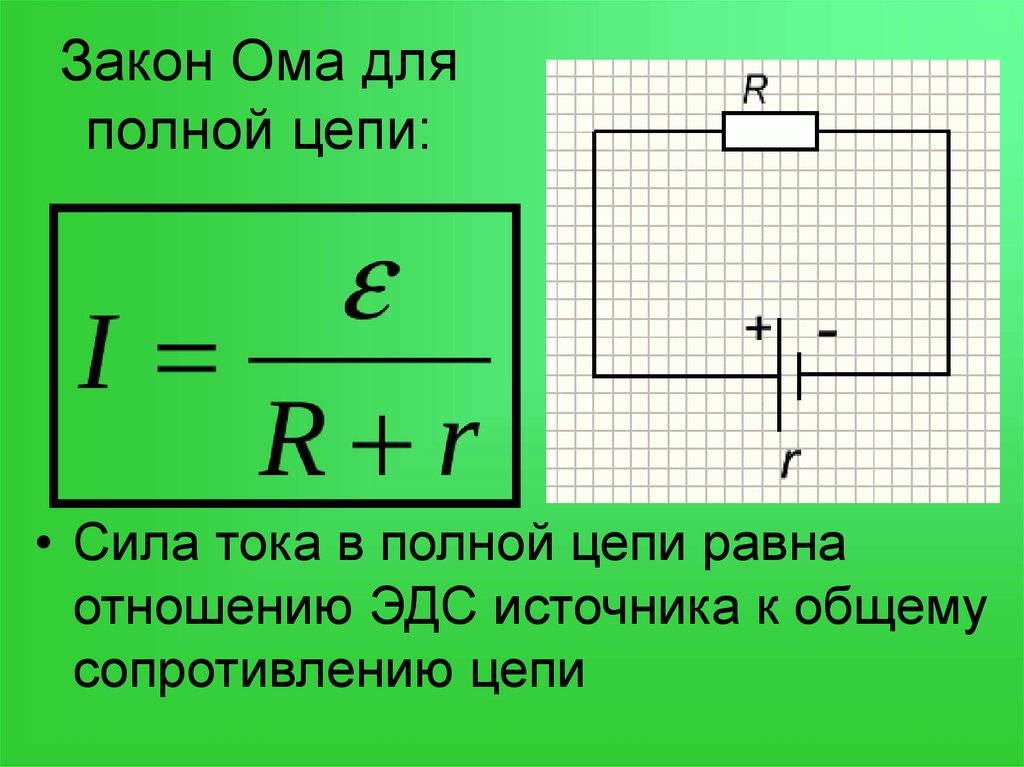
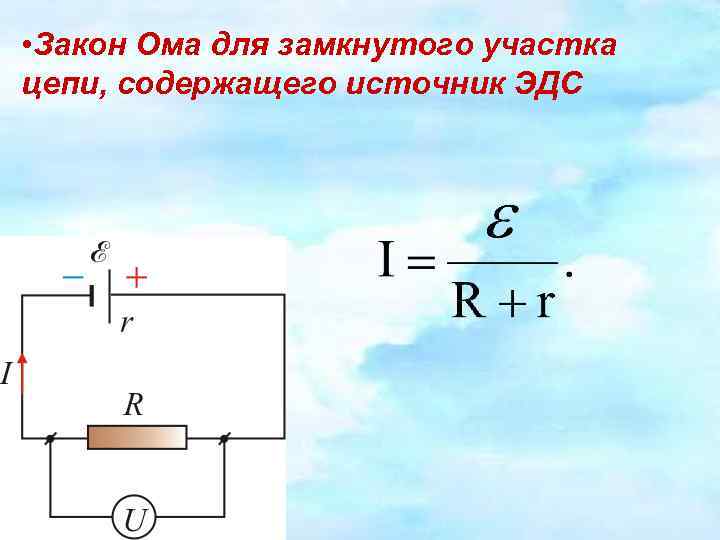
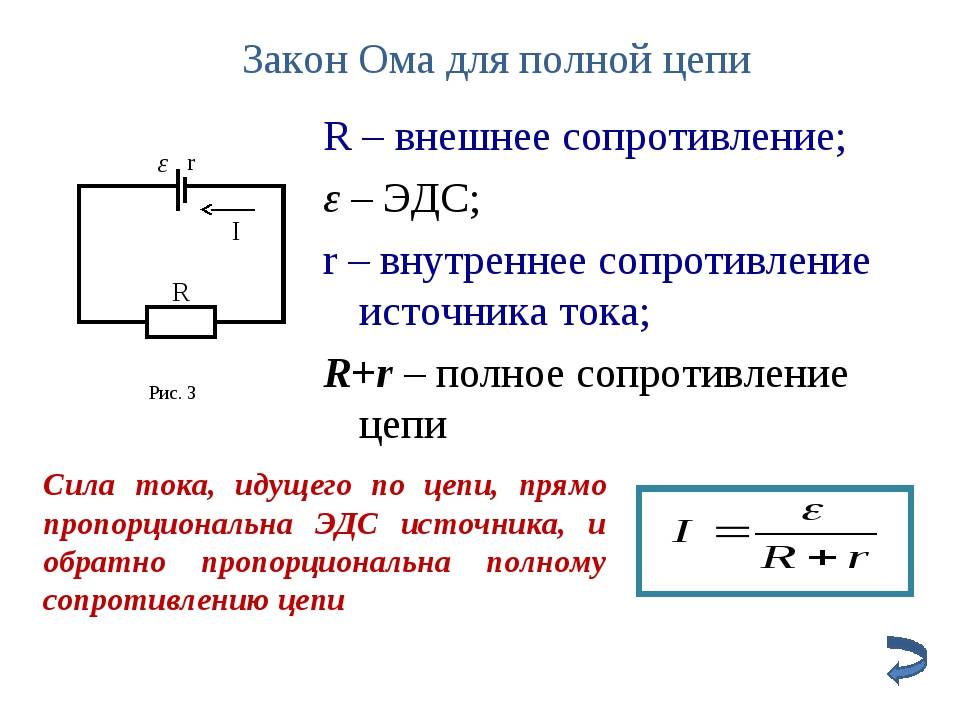
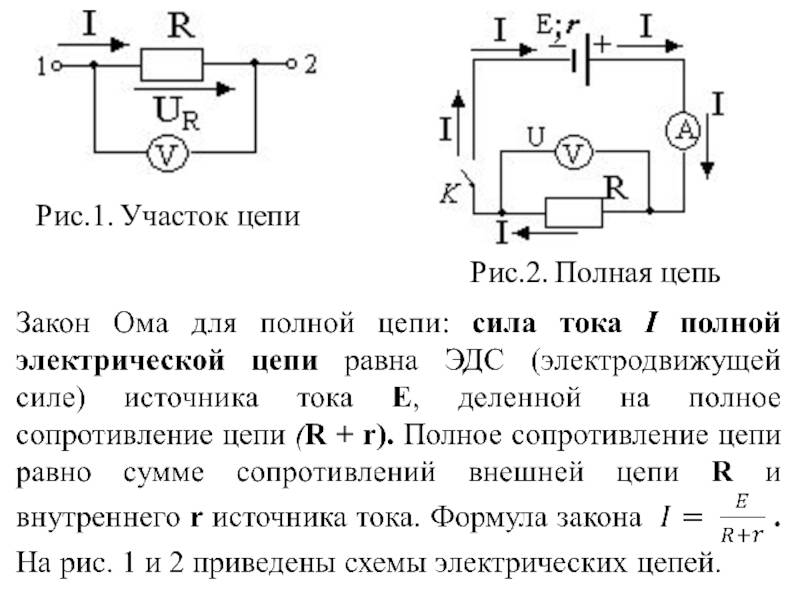
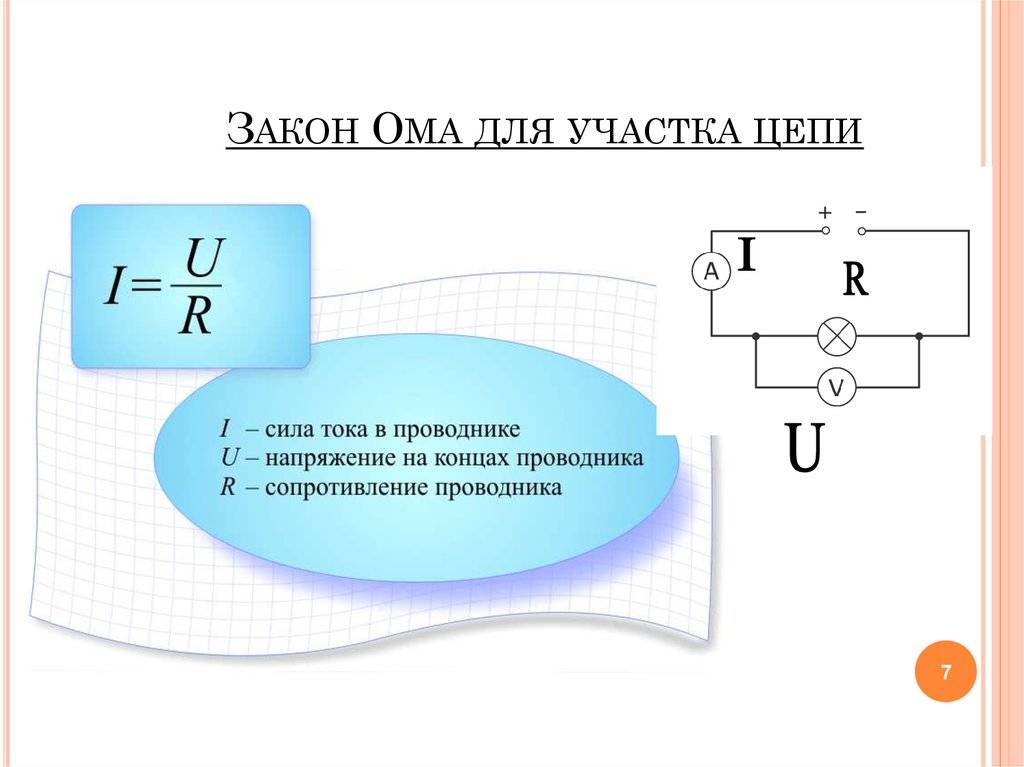
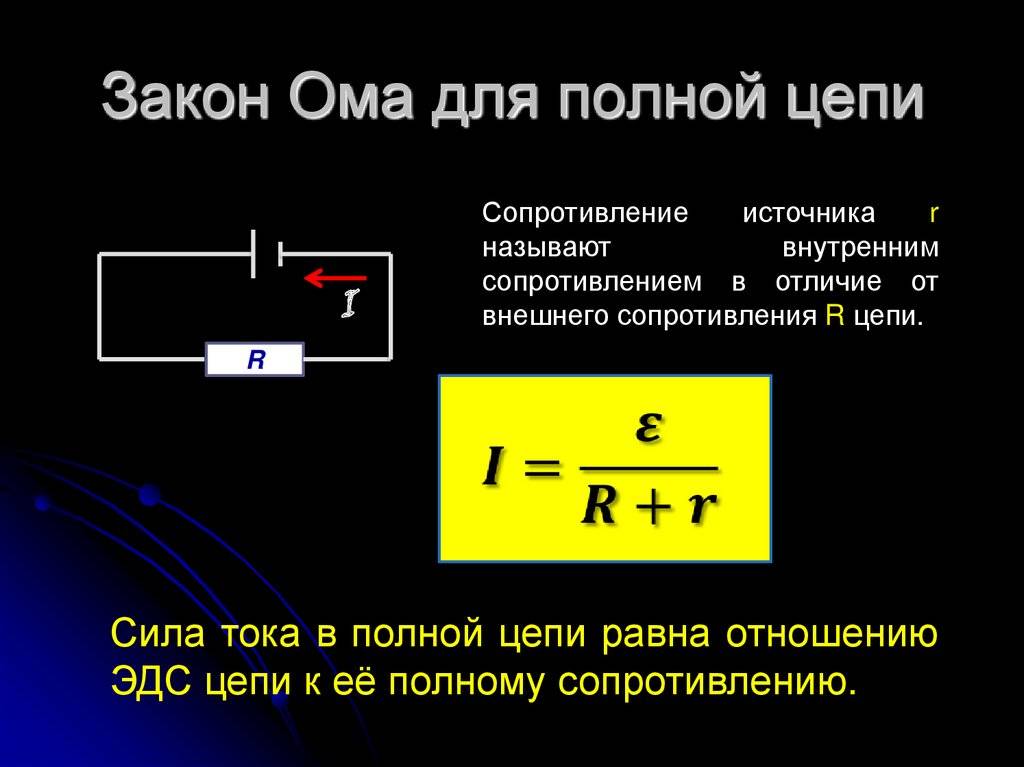
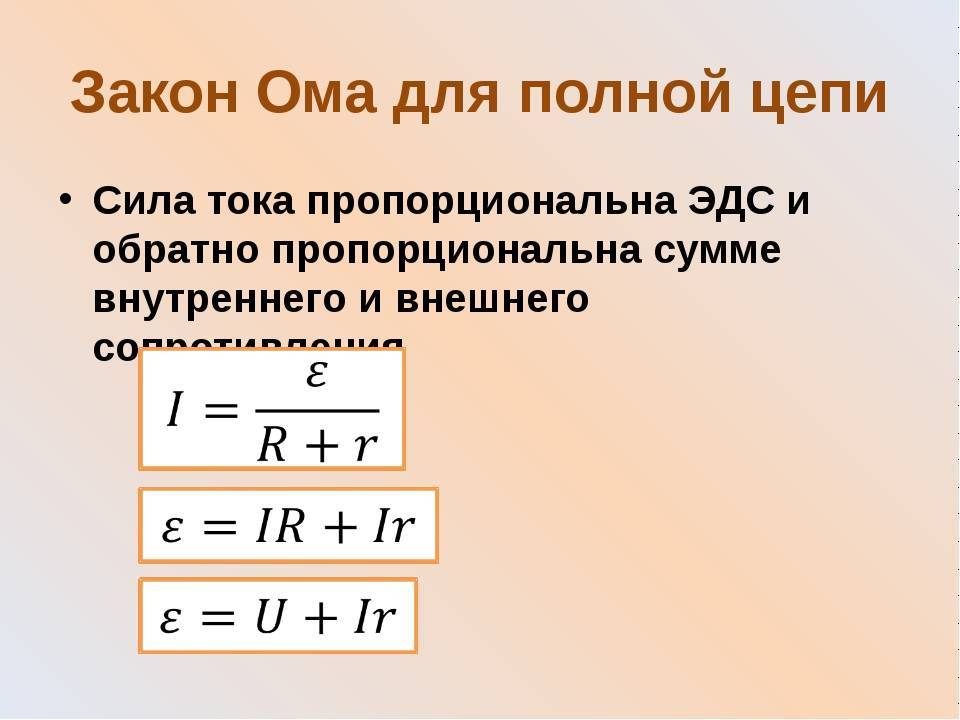
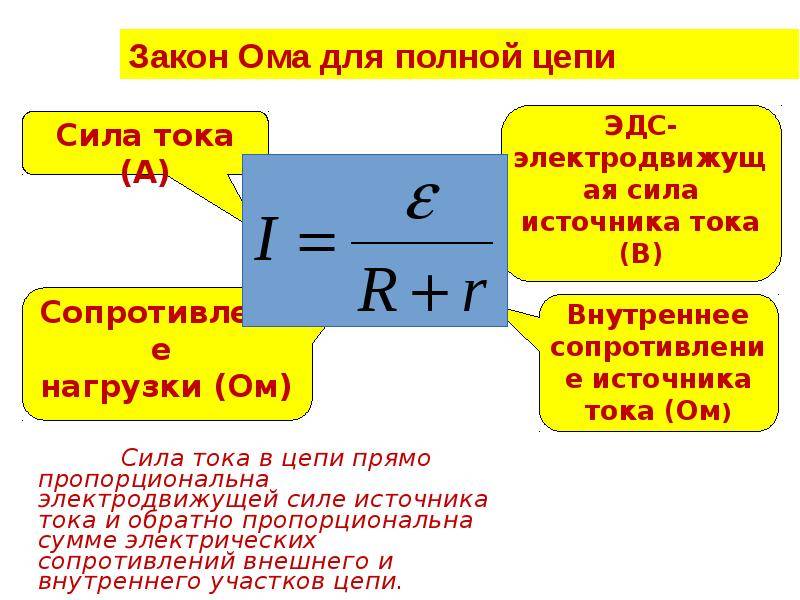
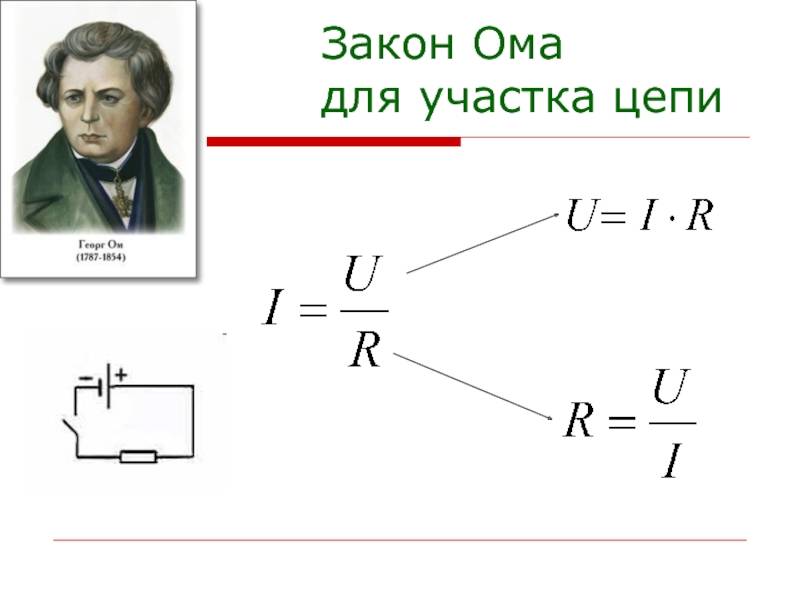
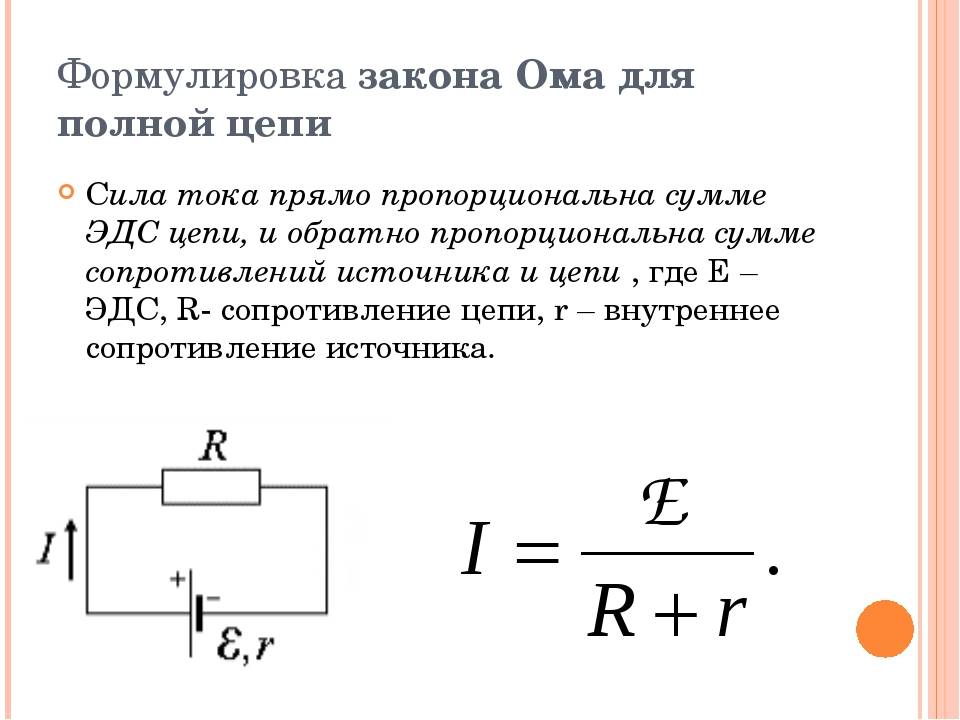
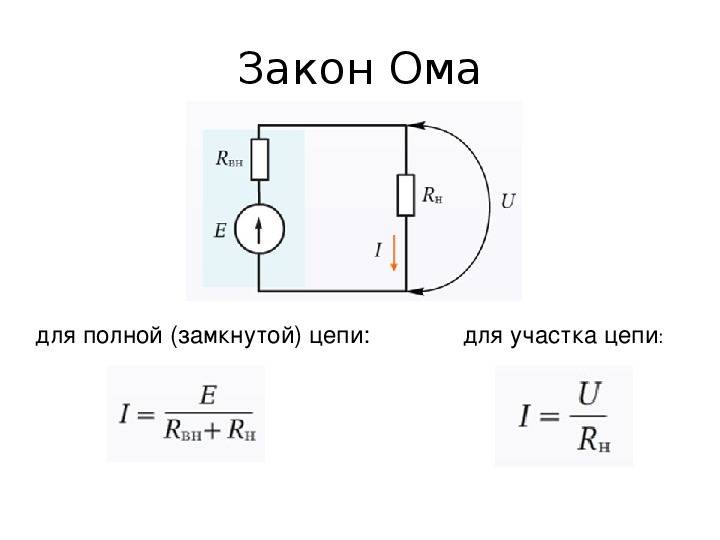
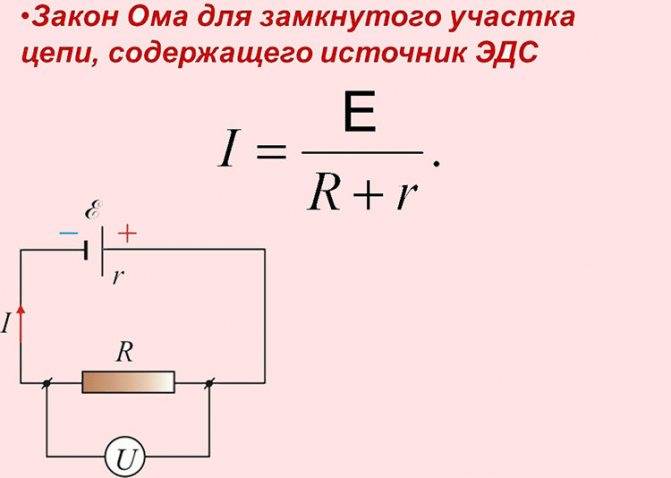
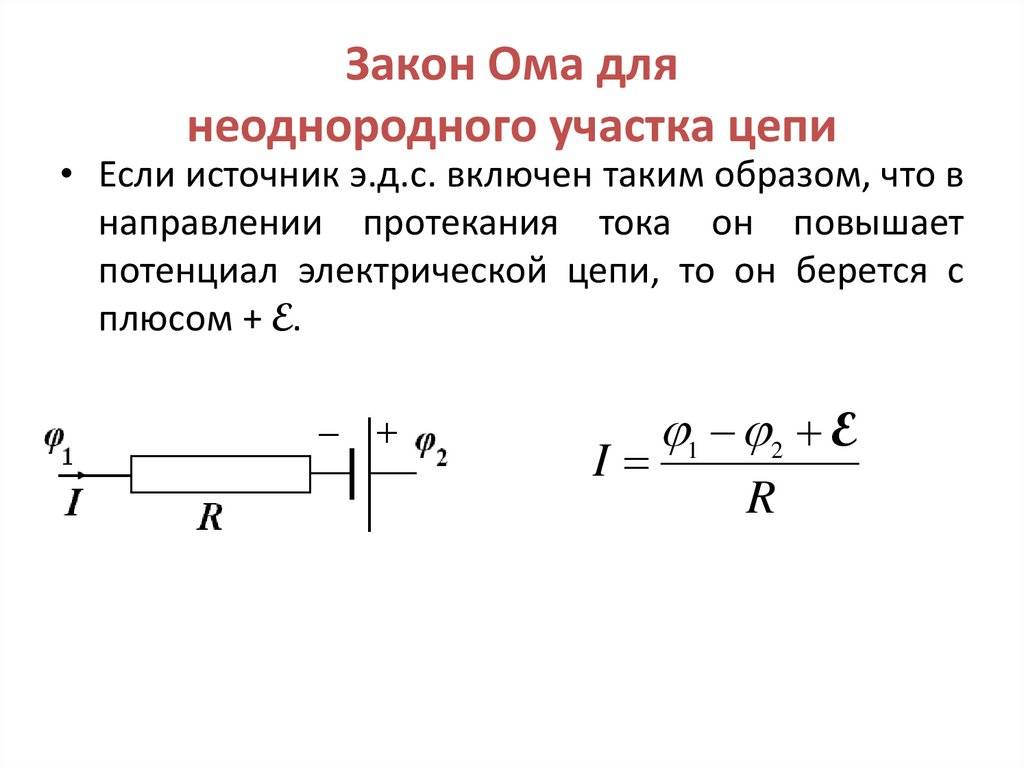
Параллельное и последовательное соединение

Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.

	Последовательное соединение	Параллельное соединение
Схема	Резисторы следуют друг за другом	Между резисторами есть два узла Узел — это соединение трех и более проводников
Сила тока	Сила тока одинакова на всех резисторах I = I1 = I2	Сила тока, входящего в узел, равна сумме сил токов, выходящих из него I = I1 + I2
Напряжение	Общее напряжение цепи складывается из напряжений на каждом резисторе U = U1 + U2	Напряжение одинаково на всех резисторах U = U1 = U2
Сопротивление	Общее сопротивление цепи складывается из сопротивлений каждого резистора R = R1 + R2	Общее сопротивление для бесконечного количества параллельно соединенных резисторов 1/R = 1/R1 + 1/R2 + … + 1/Rn Общее сопротивление для двух параллельно соединенных резисторов R = (R1 * R2)/R1 + R2 Общее сопротивление бесконечного количества параллельно соединенных одинаковых резисторов R = R1/n

Зачем нужны эти соединения, если можно сразу взять резистор нужного номинала? Начнем с того, что все электронные компоненты изготавливаются по ГОСТу. То есть есть определенные значения резисторов, от которых нельзя отойти при производстве. Это значит, что не всегда есть резистор нужного номинала и его нужно соорудить из других резисторов. Параллельное соединение также используют, как «запасной аэродром»: когда на конечный результат общее сопротивление сильно не повлияет, но в случае отказа одного из резисторов, будет работать другой. Признаемся честно: схемы, которые обычно дают в задачах (миллион параллельно соединенных резисторов, к ним еще последовательный, а к этому последовательному еще миллион параллельных) — в жизни не встречаются. Но навык расчета таких схем впоследствии упрощает подсчет схем реальных, потому что так вы невооруженным глазом отличаете последовательное соединение от параллельного.

Решим несколько задач на последовательное и параллельное соединение.

Задачка раз

Найти общее сопротивление цепи.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом

Ответ: общее сопротивление цепи равно 10 Ом

Задачка два

Найти общее сопротивление цепи.

R1 = 4 Ом, R2 = 2 Ом

Решение:

Общее сопротивление при параллельном соединении рассчитывается по формуле:

R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом

Ответ: общее сопротивление цепи равно 1 ⅓ Ом

Задачка три

Найти общее сопротивление цепи, состоящей из резистора и двух ламп.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом

Решение:

Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.

В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.

Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:

Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + Rламп = 1 + 1,2 = 2,2 Ом

Ответ: общее сопротивление цепи равно 2,2 Ом.

Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи .

Задачка четыре со звездочкой

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Решение:

Найдем сначала сопротивление лампы.

Rлампы = R/2 = 10/2 = 5 Ом

Теперь найдем общее сопротивление двух параллельно соединенных резисторов.

Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом

И общее сопротивление цепи равно:

R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом

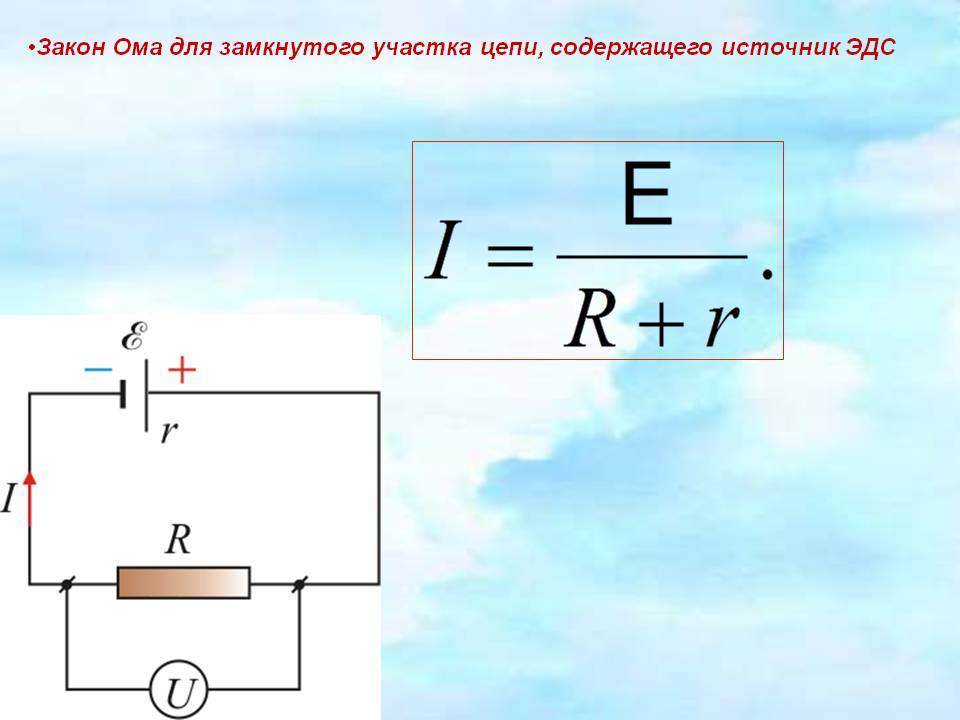
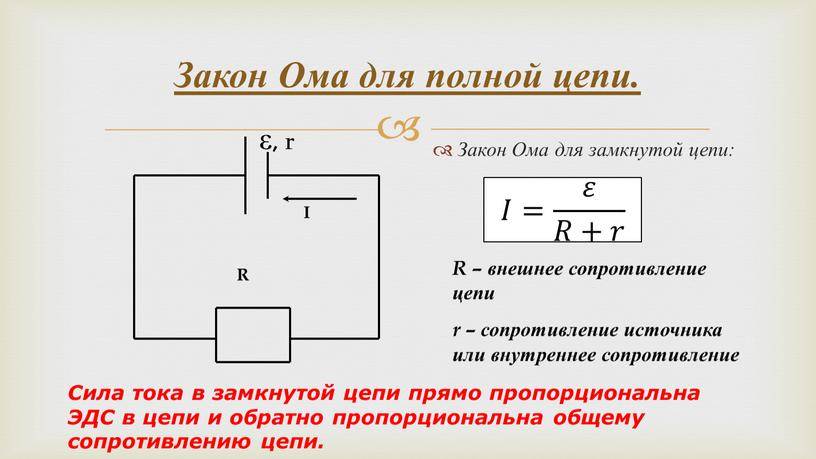
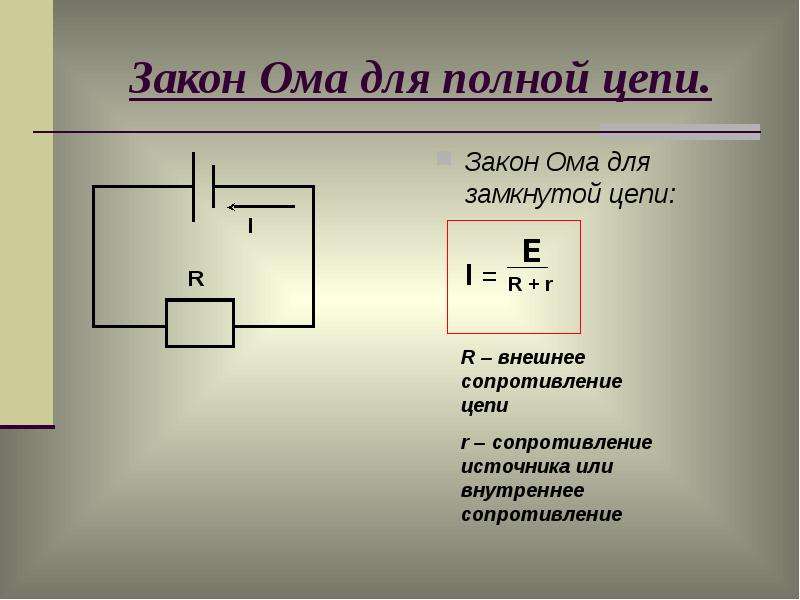
Выразим внутреннее сопротивление источника из закона Ома для полной цепи.

I = ε/(R + r)

R + r = ε/I

r = ε/I — R

Подставим значения:

r = 12/0,5 — 10 = 14 Ом

Ответ: внутреннее сопротивление источника равно 14 Ом.

Чему равно напряжение.

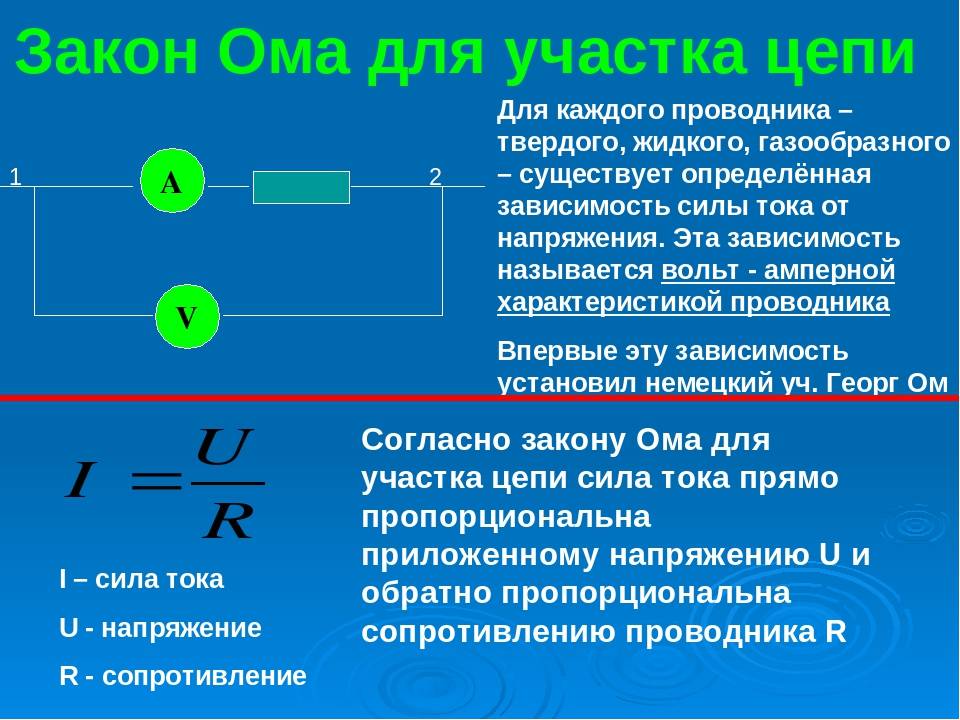
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.

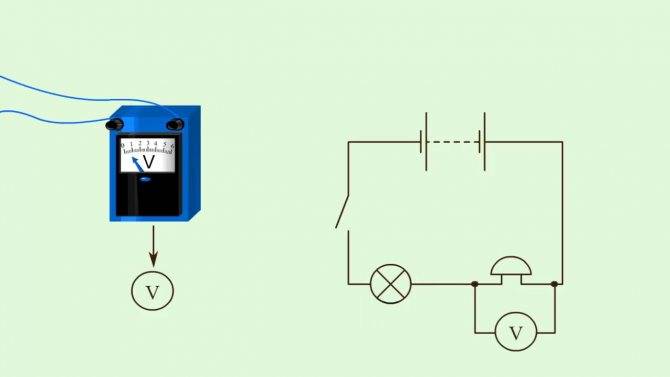
Изображение вольтметра и электрической цепи

Напряжение обозначается латинской , а измеряется в . Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.

Вам это будет интересно Чему равен 1 ампер в киловаттах

Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении. Электрическое поле

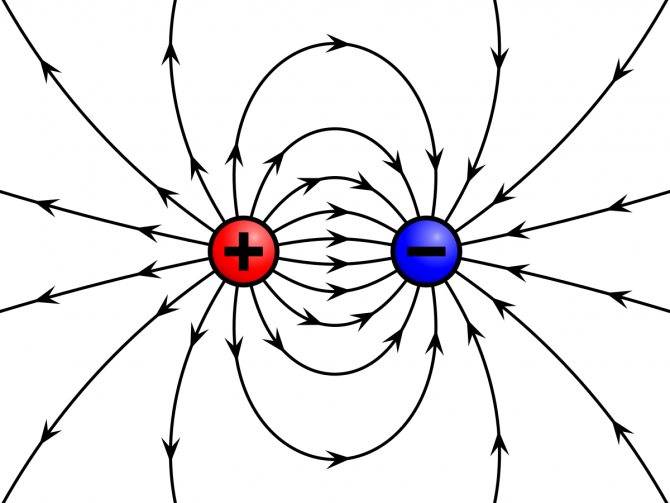
Электрическое поле

Закон Ома для всей цепи.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
  Вольтметр, подключенный к лампочке, показывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать бесконечно большим, а силу тока, текущего через вольтметр, равной нулю. 

РЕШЕНИЕ.

Задача № 2.
  Дана схема (рис. 6-11, а). Во сколько раз изменится сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л₂ вдвое больше сопротивления лампы Л₁, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л₁. 

Задача № 3.
  В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Найти силу тока короткого замыкания I_к.з. 

Задача № 4.
 Вольтметр, подключенный к полюсам источника тока при разомкнутой внешней цепи, показал U₁ = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U₂ = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить еще один такой же (рис. 6-12, б) ? Что покажет этот вольтметр, если второй резистор присоединить к первому параллельно (рис. 6-12, в)? 

Задача № 5.
  Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Построить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от внешнего сопротивления R.

Задача № 6.
  Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I₁ = 3 А . Какую силу тока I₂ покажет этот амперметр, если его зашунтировать сопротивлением R_ш = 0,1 Ом?

Задача № 7.
  Дана схема (рис. 6-16). Емкости конденсаторов С₁, С₂ и ЭДС источника тока ε известны. Известно также, что ток короткого замыкания I_к.з. этого источника в три раза превосходит ток I, текущий в этой цепи. Найти напряженности Е₁ и Е₂ полей в конденсаторах, если расстояния между их обкладками равны d. 

Задача № 8.
  Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Определить напряжения U₁ и U₂ на конденсаторах и заряды q₁ и q₂ этих конденсаторов. 

Задача № 9.
  Имеется N одинаковых источников тока, которые соединяют сначала последовательно, затем параллельно, подключая каждый раз к одному и тому же внешнему сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при этом изменяется напряжение на внешней части цепи?

Задача № 10.
 Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит посередине прибора (рис. 6-21, а). Найти показания вольтметров U₁ и U₂, подключенных к потенциометру, если их сопротивления R₁= 6 кОм и R₂ = 4 кОм. Внутренним сопротивлением r источника тока пренебречь. 

Задача № 11.
  Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Найти силу тока I₂ в сопротивлении R₂. 

Задача № 12.
  Проволока из нихрома образует кольцо диаметром D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом такой же проволокой. Найти разность потенциалов  φ_b – φ_а между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм2. 

Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

В общем, это наиболее распространенные варианты использования этих соединений.

Таблица удельных сопротивлений различных материалов

Удельное сопротивление ρ, Ом*мм2/м	Удельное сопротивление ρ, Ом*мм2/м
Алюминий	0,028
Бронза	0,095 – 0,1
Висмут	1,2
Вольфрам	0,05
Железо	0,1
Золото	0,023
Иридий	0,0474
Константан ( сплав Ni-Cu + Mn)	0,5
Латунь	0,025 – 0,108
Магний	0,045
Манганин (сплав меди марганца и никеля – приборный)	0,43 – 0,51
Медь	0,0175
Молибден	0,059
Нейзильбер (сплав меди цинка и никеля)	0,2
Натрий	0,047
Никелин ( сплав меди и никеля)	0,42
Никель	0,087
Нихром ( сплав никеля хрома железы и марганца)	1,05 – 1,4
Олово	0,12
Платина	0.107
Ртуть	0,94
Свинец	0,22
Серебро	0,015
Сталь	0,103 – 0,137
Титан	0,6
Хромаль	1,3 – 1,5
Цинк	0,054
Чугун	0,5-1,0

Ответ: нить накаливания сделана из константана.

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1 = I2 ;
• U = U1 + U2 ;
• R = R1 + R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1 + I2 … ;
• U = U1 = U2 … ;
• 1 / R = 1 / R1 + 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Практическое использование

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.Применяем закон к любому участку цепи

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.Находим силу токаРассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

• R=0,2 МОм;
• U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).Вычисление напряженияДля решения мы также воспользуемся законом, составленным Омом. Итак задача:

• R=20 кОм;
• I=10 мА.

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление.

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров.

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении

Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Источники

• https://poschitat.online/zakon-oma
• https://tel-spb.ru/ohm/
• https://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D1%82%D0%B2%D0%BE/%D1%86%D0%B5%D0%BF%D0%B8_%D0%BF%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE_%D1%82%D0%BE%D0%BA%D0%B0/%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%81%D0%BE%D0%BF%D1%80%D0%BE%D1%82%D0%B8%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5/
• https://radioprog.ru/post/920
• https://elektroznatok.ru/info/teoriya/zakon-oma
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html

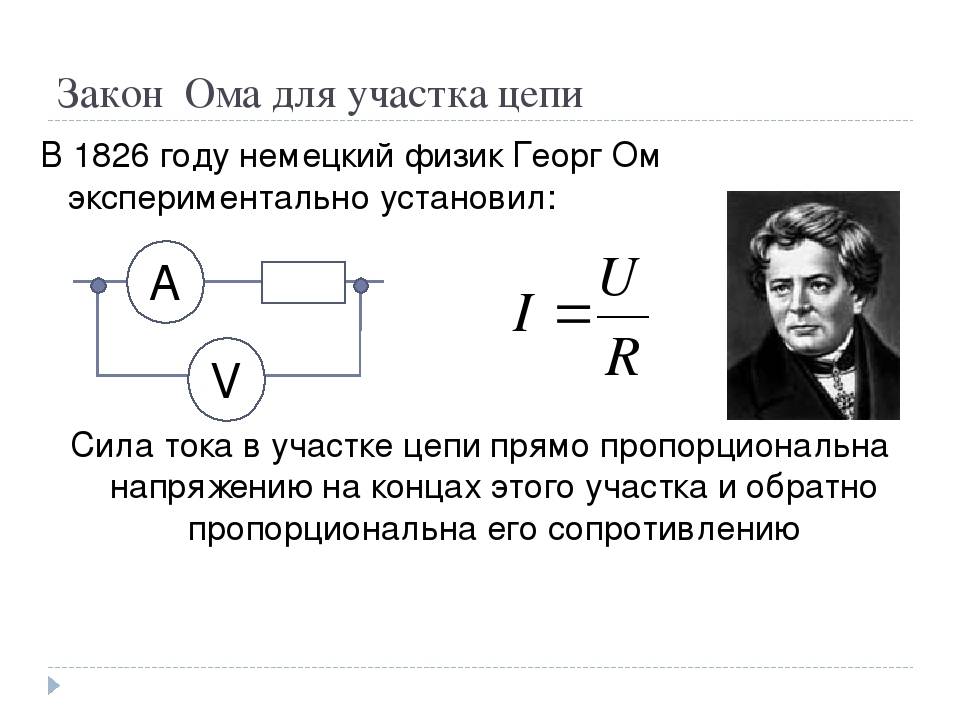
Формула Закона Ома

В 1827 году Георг Симон Ом открыл закон силы электрического тока. Его именем назвали Закон и единицу измерения величины сопротивления. Смысл закона в следующем.

Чем толще труба и больше давление воды в водопроводе (с увеличением диаметра трубы уменьшается сопротивление воде) – тем больше потечет воды. Если представить, что вода это электроны (электрический ток), то, чем толще провод и больше напряжение (с увеличением сечения провода уменьшается сопротивление току) – тем больший ток будет протекать по участку цепи.

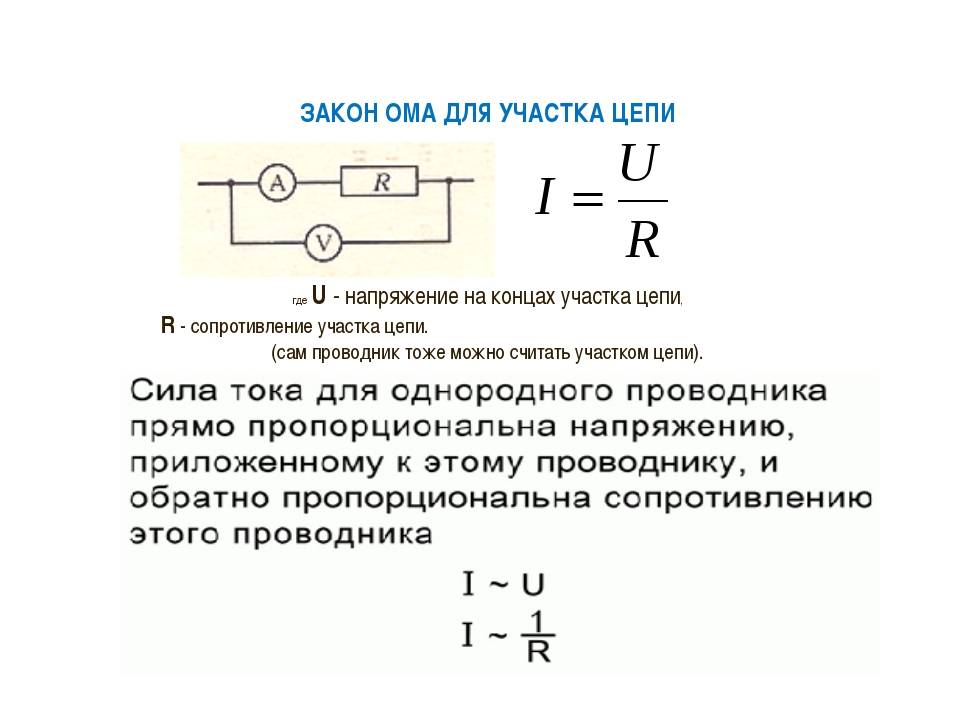
Сила тока, протекающая по электрической цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна величине сопротивления цепи.

гдеI – сила тока, измеряется в амперах и обозначается буквой А;U – напряжение, измеряется в вольтах и обозначается буквой В;R – сопротивление, измеряется в омах и обозначается Oм.

Если известны напряжение питания U и сопротивление электроприбора R, то с помощью вышеприведенной формулы, воспользовавшись онлайн калькулятором, легко определить силу протекающего по цепи тока I.

С помощью закона Ома рассчитываются электрические параметры электропроводки, нагревательных элементов, всех радиоэлементов современной электронной аппаратуры, будь то компьютер, телевизор или сотовый телефон.

Основные понятия

Электрический ток течёт, когда замкнутый контур позволяет электронам перемещаться от высокого потенциала к более низкому в цепи. Иначе говоря, ток требует источника электронов, обладающего энергией для приведения их в движение, а также точки их возвращения отрицательных зарядов, для которой характерен их дефицит. Как физическое явление ток в цепи характеризуется тремя фундаментальными величинами:

• напряжение;
• сила тока;
• сопротивление проводника, по которому движутся электроны.

Сила и напряжение

Сила тока (I, измеряется в Амперах) есть объём электронов (заряд), перемещающихся через место в цепи за единицу времени. Иными словами, измерение I — это определение количества электронов, находящихся в движении

Важно понимать, что термин относится только к движению: статические заряды, например, на клеммах неподсоединённой батареи, не имеют измеряемого значения I. Ток, который протекает в одном направлении, называется постоянным (DC), а периодически изменяющий направление — переменным (AC). Напряжение можно проиллюстрировать таким явлением, как давление, или как разность потенциальной энергии предметов под воздействием гравитации

Для того чтобы создать этот дисбаланс, нужно затратить предварительно энергию, которая и будет реализована в движении при соответствующих обстоятельствах. Например, в падении груза с высоты реализуется работа по его подъёму, в гальванических батареях разность потенциалов на клеммах образуется за счёт преобразования химической энергии, в генераторах — в результате воздействия электромагнитного поля

Напряжение можно проиллюстрировать таким явлением, как давление, или как разность потенциальной энергии предметов под воздействием гравитации. Для того чтобы создать этот дисбаланс, нужно затратить предварительно энергию, которая и будет реализована в движении при соответствующих обстоятельствах. Например, в падении груза с высоты реализуется работа по его подъёму, в гальванических батареях разность потенциалов на клеммах образуется за счёт преобразования химической энергии, в генераторах — в результате воздействия электромагнитного поля.

Советуем изучить Производственное освещение виды производственного освещения. виды освещения — охрана труда на предприятии

Сопротивление проводников

Независимо от того, насколько хорош обычный проводник, он никогда не будет пропускать сквозь себя электроны без какого-либо сопротивления их движению. Можно рассматривать сопротивление как аналог механического трения, хотя это сравнение не будет совершенным. Когда ток протекает через проводник, некоторая разность потенциалов преобразуется в тепло, поэтому всегда будет падение напряжения на резисторе. Электрические обогреватели, фены и другие подобные устройства предназначены исключительно для рассеивания электрической энергии в виде тепла.

Упрощённо сопротивление (обозначается как R) является мерой того, насколько поток электронов тормозится в цепи. Оно измеряется в Омах. Проводимость резистора или другого элемента определяется двумя свойствами:

• геометрией;
• материалом.

Форма имеет важнейшее значение, это очевидно на гидравлической аналогии: протолкнуть воду через длинную и узкую трубу гораздо тяжелее, чем через короткую и широкую. Материалы играют определяющую роль. Например, электроны могут свободно перемещаться в медном проводе, но не способны протекать вообще через такие изоляторы, как каучук, независимо от их формы. Кроме геометрии и материала, существуют и другие факторы, влияющие на проводимость.

Идеальный источник ЭДС

Электродвижущая сила (E) – физическая величина, определяющая степень воздействия внешних сил на перемещение в замкнутой цепи носителей заряда. Иными словами, от ЭДС будет зависеть то, как сильно ток стремится течь по проводнику.

При объяснении подобных непонятных явлений отечественные школьные учителя любят обращаться к методу гидравлических аналогий. Если проводник – это труба, а электрический ток – это количество протекающей по ней воды, то ЭДС – это давление, которое развивает насос, чтобы качать жидкость.

Термин электродвижущая сила родственен такому понятию, как напряжение. Она, ЭДС, так же измеряется в вольтах (ед. изм. – «В»). Каждый источник питания, будь то батарейка, генератор или солнечная панель, обладает своей собственной электродвижущей силой. Зачастую эта ЭДС близка к выходному напряжению (U), но всегда немного меньше его. Вызвано это внутренним сопротивлением источника, на котором неизбежно падает часть вольтажа.

По этой причине идеальный источник ЭДС – это скорее абстрактное понятие или физическая модель, не имеющая места в реальном мире, ведь внутреннее сопротивление элемента питания Rвн хоть и весьма низкое, но всё же отлично от абсолютного нуля.

Идеальный и реальный источник ЭДС

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Отдельный участок и полная электрическая цепь

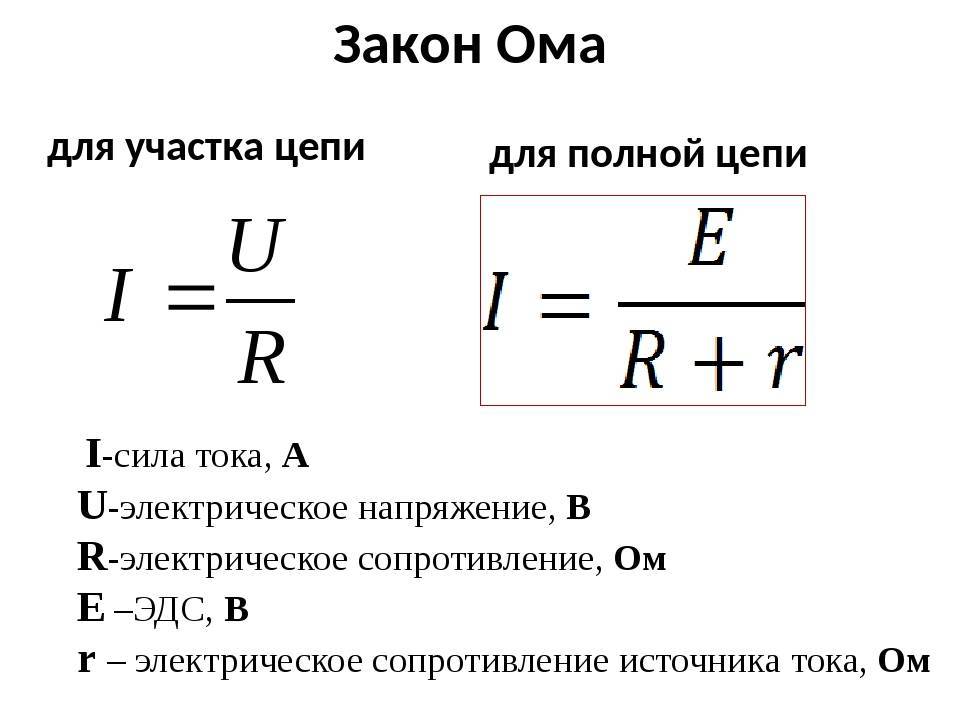
Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:

• Отдельный краткий участок. Является частью схемы без источника ЭДС.
• Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.

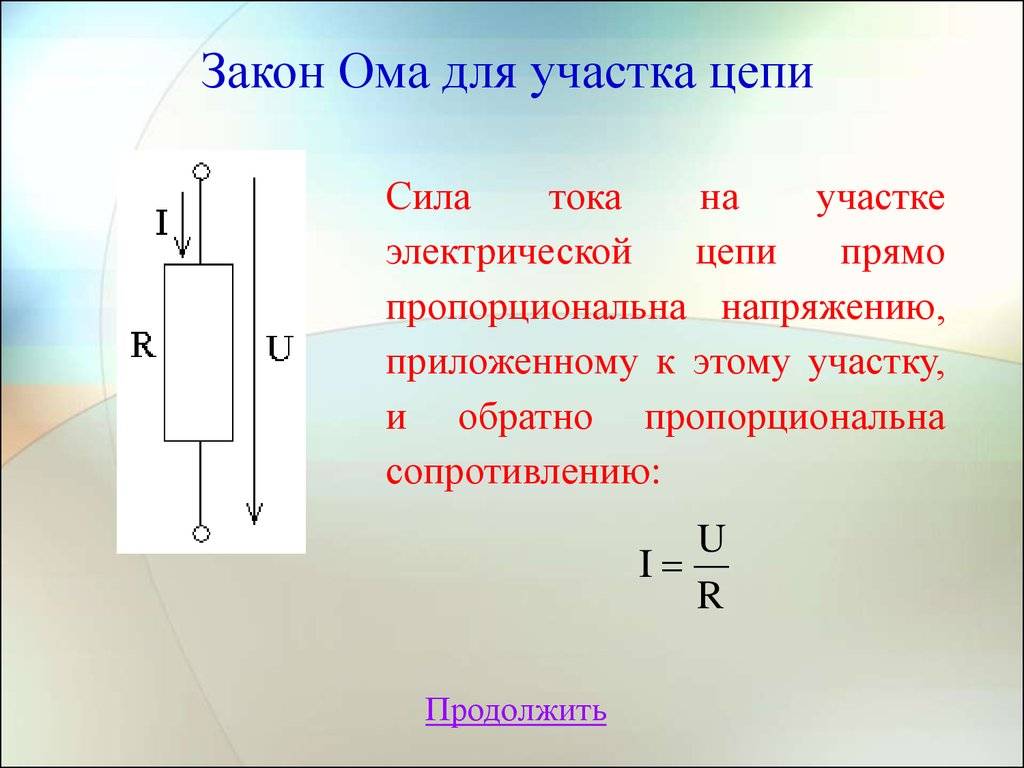
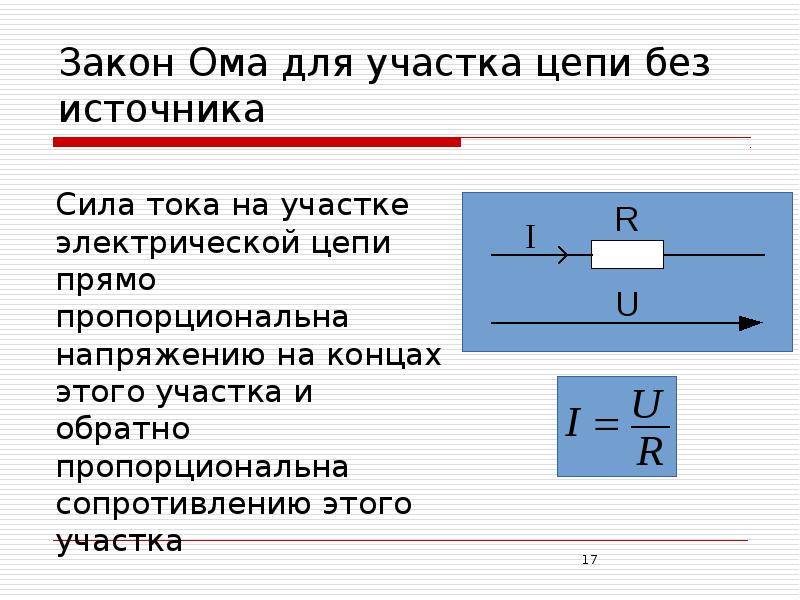
Расчет тока участка электрической схемы

В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:

Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.

Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.

Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.

В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.

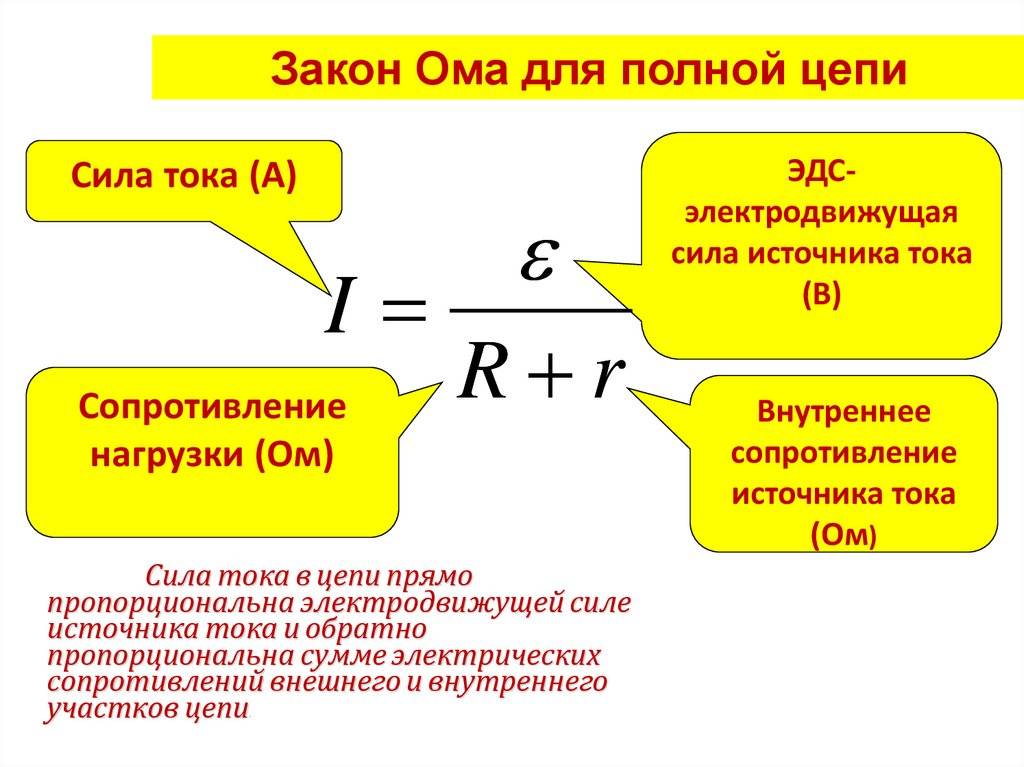
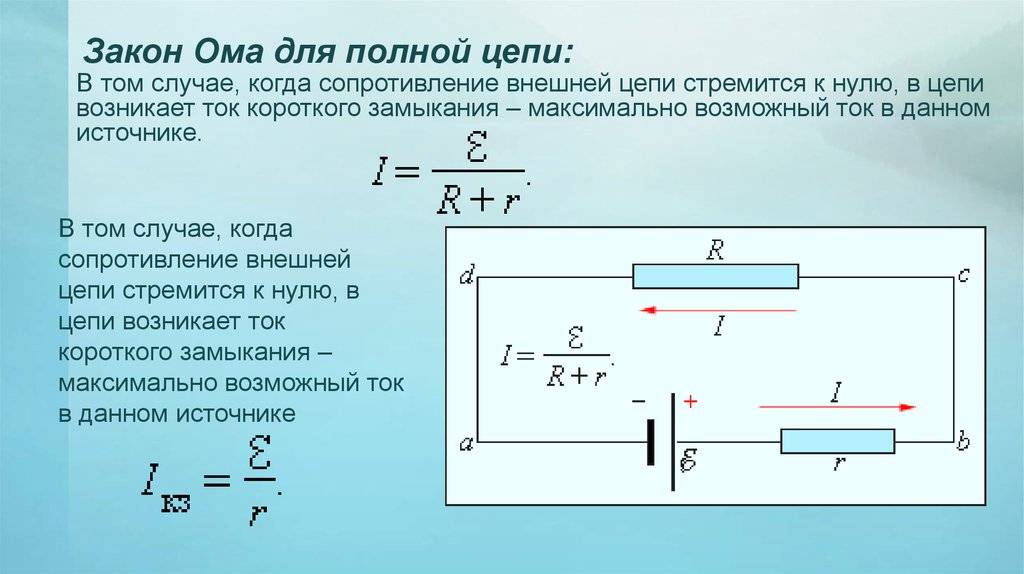
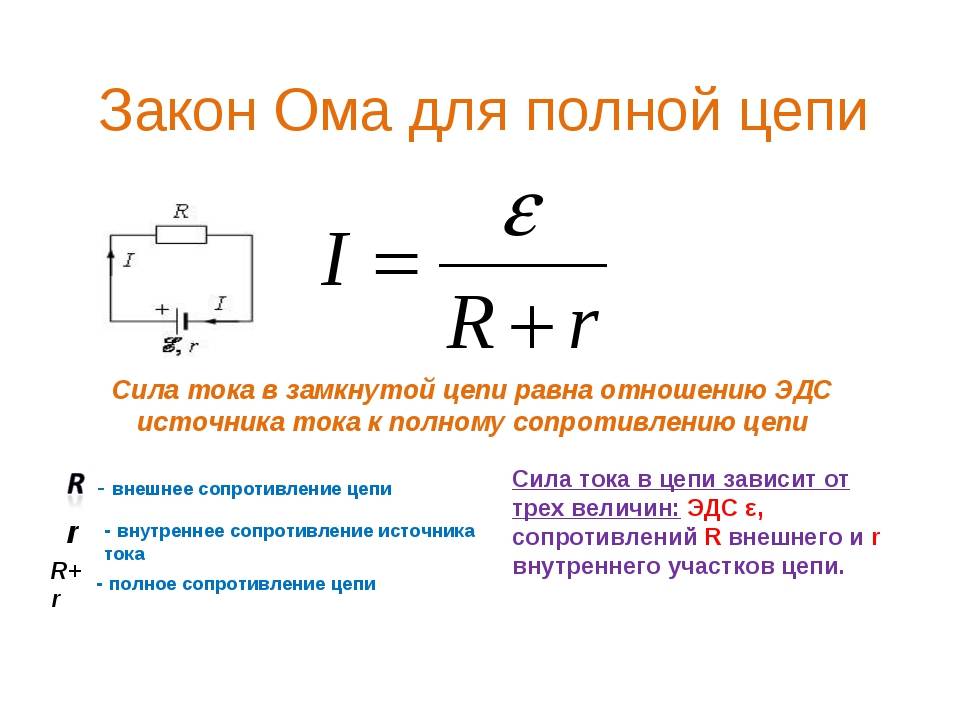
Вариант расчета для полной цепи

Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.

С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.

Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.

Действие закона к переменной величине

При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.

Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.

Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.

Выводы и полезное видео по теме

Подробный разбор закона Ома в видеоролике, представленном ниже, поможет окончательно закрепить знания в этом направлении.

Своеобразный видеоурок качественно подкрепляет теоретическое письменное изложение:

Работа электрика или деятельность электронщика неотъемлемо связана с моментами, когда реально приходится наблюдать закон Георга Ома в действии. Это своего рода прописные истины, которые следует знать каждому профессионалу.

Объёмных знаний по данному вопросу не требуется – достаточно выучить три основных вариации формулировки, чтобы успешно применять на практике.

Хотите дополнить изложенный выше материал ценными замечаниями или выразить свое мнение? Пишите, пожалуйста, комментарии в блоке под статьей. Если у вас остались вопросы, не стесняйтесь задавать их нашим экспертам.